Mais qu’est-ce que c’est que ce truc ? Rassurez-vous je ne parlerai ni de ket, ni d’espace de Hilbert, ni même de vecteurs propres (quoique…).
Bien loin d’un chat mort-vivant, Heisenberg a réussi à montrer des choses inquiétantes. Certains l’interprètent comme une interdiction divine de tout savoir, alors que d’autres y voient une magnifique convergence entre les mathématiques et l’expérience physique.
Nos amis physiciens quanticiens (oui ce mot existe !) sont limités par une petite inégalité de rien du tout.
Pré-requis : Mouche Vs Mamie
Pour comprendre cela, il est nécessaire de savoir ce qu’est une quantité de mouvement (aussi appelée « impulsion ») :
– Imaginons une seconde qu’une mouche, dans sa course à votre assiette, vole à 20km/h (c’est-à-dire 5,6m/s) et vous percute de plein fouet ! Rien de bien fou.
– Imaginons cette fois qu’une voiture roule à 20km/h (oui c’est une personne âgée) et vous percute de plein fouet ! On fait moins le malin ?
Vous l’avez compris, entre les 20mg de notre petit insecte et les 1000kg de la voiture de mémé, ça change tout. Bon et bien la quantité de mouvement c’est simplement le produit de la vitesse (en m/s) et de la masse (en kg).
- Pour la mouche : p = 0,000112 kg.m/s
- Pour la voiture : p = 5600 kg.m/s
Et là on se rend compte que l’un des deux est bien plus violent que l’autre. Compris ? (pour ceux que ça intéresse, vous ressentirez l’énergie cinétique qui vaut p²/2m)
Et du coup, le Principe d’Heisenberg ?
2 points sont vraiment beaux dans le Principe d’Incertitude :
- Ce n’est pas un principe, mais une relation (puisqu’on peut le démontrer).
- Il démontre que nous sommes incapables d’avoir une haute précision sur deux grandeurs simultanément.
Rentrons dans les mathématiques assez brièvement.
2 x 3 = 6. Tout le monde est d’accord ?
3 x 2 = 6 aussi.
Donc 3 x 2 = 2 x 3.
On appelle ça « commuter », c’est à dire inverser l’ordre des grandeurs dans le calcul. Ici on inversait 3 et 2, ça ne changeait rien.
Malheureusement, ces grandeurs (dîtes scalaires) ont la fâcheuse habitude de donner de faux espoirs. Parce que pour bien comprendre quelque chose de petit (vraiment très très petit), il est nécessaire d’utiliser des Observables. Attention, quand je dis petit, il faut bien avoir en tête qu’un microbe c’est très gros, une goutte d’eau c’est immense, un électron c’est petit, un atome, c’est plutôt petit, une molécule c’est déjà limite (cf diffraction du fullerène, c’est assez impressionnant). En gros, ce sont des matrices. Voila une matrice, prise au hasard :
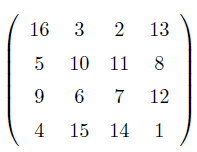
Voila à quoi ressemble une matrice, prise au hasard. C’est une sorte de tableau, sur lequel on peut faire plein de calculs mathématiques.
Vous connaissiez « les chiffres » (de 0 à 9), les entiers (de 10, 11, 12, …). Et bien voila les matrices. Il s’agit d’un objet mathématique un peu plus complexe, mais très utilisé. Comme avec des nombres, on peut soustraire des matrices entre elles, les additionner, les multiplier, etc. Pour multiplier des matrices, il existe une méthode bien précise, mais qu’on n’expliquera pas ici.
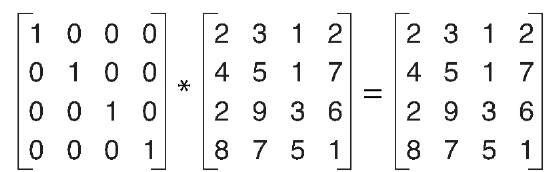
Comme on peut multiplier « 3 » et « 2 » pour donner « 6 », il est possible de multiplier 2 matrices entre elles pour donner une matrice résultante (vous noterez, pour les curieux/matheux que celle de gauche est appelée « élément neutre de la multiplication », c’est l’équivalent du « 1 » dans les nombres que l’on utilise tous les jours, qui ne fait aucune modification quand on l’utilise pour multiplier).
Mais contrairement à des grandeurs scalaires (comme les chiffres 3 et 2 par exemple), les matrices ne sont pas commutables. Cela veut dire que si vous voulez multiplier 2 matrices entre elles, il faudra bien faire attention à l’ordre du calcul.
Disons que votre première matrice s’appelle X, et votre seconde matrice s’appelle P. Alors faire « X fois P » ne donnera pas le même résultat que « P fois X ». Ça peut paraître bizarre, parce qu’on a vu toute à l’heure que « 3×2 = 2×3 ». Mais ce qui vaut pour les chiffres ne vaut pas toujours pour les matrices.
Donc XP n’est pas égal à PX. Et ça, ça pose problème. En mécanique quantique, c’est directement visible sur l’ordre dans lequel vous prenez vos mesures. Ainsi dire « P fois X » revient à dire : « Je mesure P, puis je mesure X et je les multiplie dans cet ordre ».
D’ailleurs, vous noterez que votre système peut évoluer entre une mesure et une autre. Prenez par exemple l’écran de votre téléphone portable et essayez de mesurer sa surface. Il vous suffira de mesurer la longueur et la largeur de l’écran, et de les multiplier. Puisque l’écran ne bouge pas, le résultat sera toujours le même (il est dit déterministe).
Maintenant essayez de mesurer la surface de cheveux sur la tête de Psy dans son clip Gangnam Style, le tout sans appuyer sur pause. C’est bien plus complexe car le temps que vous fassiez une première mesure de longueur, le plan de la caméra aura changé et votre seconde mesure sera biaisée. C’est un peu ce qui se passe dans un calcul, lorsque des mesures ne commutent pas : en fonction de votre manière de calculer, vous trouverez des résultats différents.
Venons en au fait : si on appelle 
l’erreur de position que vous pouvez commettre pendant la mesure et 
l’erreur de quantité de mouvement. On se rend compte mathématiquement et physiquement que 
.
Où 
désigne la constante de Planck réduite. Et ça, c’est le principe d’incertitude d’Heisenberg, ou plutôt le Théorème d’Indétermination d’Heisenberg.
Si vous voulez aller plus loin
– Cette inégalité est valable avec beaucoup de grandeurs complémentaires (position/impulsion, moment cinétique/position angulaire, moment cinétique selon un axe/moment cinétique selon un autre axe, temps/énergie, largeur spectrale/largeur temporelle d’une transformée de Fourier)
– En vulgarisant, on a tendance à entendre que la mesure va modifier le résultat de la prochaine mesure et donc qu’il devient impossible d’inverser les deux mesures. C’est faux. La preuve mathématique ne fait nullement mention de mesures. Cette inégalité est intrinsèque à la physique quantique.
– Albert Einstein s’y est beaucoup opposé, je vous invite à vous renseigner sur la controverse de Bohr-Einstein.
Démonstration à la main pour les curieux
Une démonstration possible, il en existe des plus mathématiques basées sur les transformées de Fourier
6 Commentaires
antonio de la vega
31 mai 2017 à 14 h 53 minBravo, c’est un sujet qui m’intéresse et que tu maitrises visiblement ! chapeau pour l’effort de vulgarisation sans sacrifier les vrais résultats mathématiques ..
Par contre moi qui connait UN PEU le sujet (moins que toi, j’ai juste lu quelques livres sur le sujet) je pensais que le problème du chat mort venait à la fois du caractère probabiliste des situations quantiques, et aussi du fait de la mesure, un peu comme si tant que l’on ne tirait pas une boule au sort, toutes les boules possibles étaient dans des états superposés ..mais cette facette n’apparait pas, et bien que je crois tes explications mathématiques, n’aurait il pas un autre moyen de l’expliquer ?
Merci en tout cas et a bientôt
Quentin Gcn
31 mai 2017 à 23 h 20 minMerci pour les compliments 😀
L’article ne portait pas spécialement sur le Chat de Schrödinger mais si tu veux en discuter, n’hésite pas à venir sur Slack ou à répondre ici.
Le chat, comme tu le sais, n’est pas une véritable expérience mais une vue de l’esprit.
Les états superposés sont le propre du quantique en effet. Il s’agit des coefficients devant les états propres correspondant qui, élévés au carré, te donne la probabilité d’observer tel ou tel état.
En effet, c’est la mesure seule qui détermine le résultat avec certitude. Cependant, le résultat de cette mesure est probabiliste, c’est-à-dire que deux mesures du même phénomène te donneront des résultats différents.
Physiquement, pour s’éloigner un peu des mathématiques, considère que l’électron n’existe même pas et n’est pas visible. On représente alors la probabilité de sa présence par une fonction d’onde qui rend compte de ses caractéristique physique. Celle-ci est liée à l’énergie potentielle et cinétique de ta particule (le Hamiltonien) par la relation de Schrodinger H Psi = E Psi où E apparait come une valeur propre de H associée à Psi.
C’est difficile d’être beaucoup plus physique. Après j’admet qu’une bonne compréhension n’est pas évidente sans quelques bases d’algèbre linéaire.
louisrubikraft
10 juillet 2017 à 1 h 03 minSalutations !
Un article intéressant, qui m’a appris des choses. En particulier, j’apprécie ta façon de comprendre l’impulsion !
Une remarque cependant, dont je souhaite discuter (je ne suis pas totalement certain de ce que je dis) :
La conséquence de la non commutativité de deux observables implique physiquement qu’il est improbable d’obtenir le même résultat en mesurant d’abord la première puis la seconde, ou la seconde puis la première, puisque le propre de l’observable appliquée sur un ket est de fournir un nouveau ket état propre de l’observable. Ainsi, appliquer la première observable modifie le système, puis appliquer la seconde le modifie de nouveau. Comme tu le mentionnes, la mesure ne modifie en effet pas le résultat de la prochaine mesure, mais bien l’état du système lui-même. Mais la preuve mathématique de l’inégalité de Heisenberg exploite bien ce fait : [X,P] non nul signifie bien que les observables ne commutent pas signifie bien que X et P ne peuvent être mesurées en même temps sans indétermination.
Il m’apparaît ainsi important de remarquer que si deux observables ne commutent pas, cela ne signifie tout de même pas que si on mesure la position d’une particule, il devient impossible de mesurer sa vitesse : c’est possible plus tard, mais juste pas au même moment. [X,P] non nul signifie donc qu’il n’est pas possible de mesurer X et P en même temps, d’où la relation d’indétermination d’Heisenberg.
Cependant, on notera qu’il existe des observables qui commutent, bien sûr : si je regarde les positions de deux particules non couplées, je peux faire la mesure en même temps pour les deux. Et il y en a beaucoup d’autres, hein.
Je n’ai pas bien compris ton analogie avec la mesure de la longueur des cheveux, qui le semble avoir trait à l’incertitude d’une mesure et non pas à l’indétermination sur la mesure.
Question sur ta démo écrite : pourquoi as-tu écrit $P(\lambda)$ de cette façon ? Cela ne me semble pas évident du tout.
Et petit erratum dans ta démo écrite dans ton écriture de $\Delta A$ : il manque une racine carrée si je ne m’abuse ^^
quentingarcon
10 juillet 2017 à 12 h 40 minOuais pour la démo j’ai zappé la racine pour écart-type/variance.
P (lambda) ? Parce que la variable X aurait porté à confusion
La forme quant à elle, simplement pour « rendre hommage » aux inégalités habituelles de type Cauchy-Schwarz.
Merci pour ton appréciation !
Pour la commutativité, il devenait hors de question d’entrer dans des détails mathématiques plus précis, le but reste bien de donner un aperçu, de faire comprendre le principe et les grandes lignes. L’idée que j’essaye de transmettre est celle ci : Seule la mesure est probabiliste, tout le reste est déterministe (contrairement aux idées reçues).
L’analogie a certes un point faible mais j’en avais conscience : le fait que le système évolue alors qu’en PQ le problème vient de la simultanéité de la mesure. Cependant, je trouvais intéressant de prendre un cas de la vie de tous les jours pour rendre compte de ce type d’inégalité.
J’ai aussi pensé à dire : prenez une mouche en photo, vous avez sa position mais vous l’avez figée donc vous perdez la vitesse. Mais le point faible de cette analogie reste identique. Il est difficile d’appliquer une inégalité quantique sur du classique sans se permettre des petites libertés, tu t’en doutes 😉
Enfin pour ce qu’il s’agit des kets, la portion du public capable de lire la démo et connaissant les ket n’ont pas besoin de cette vulgarisation et savent l’aspect physique qui se cache derrière. La démo est plus là pour « faire joli » et montrer que l’inégalité est justifiable que pour être lue. En toute honnêteté, sans avoir étudié le domaine, ça ferait peur !
Jérôme
5 août 2017 à 20 h 41 minBonjour à tous,
Merci beaucoup pour cet excellent article!
C’est très appréciable d’avoir des articles de ce genre qui permettent de présenter des concepts très pointus au plus grand nombre et surtout bien expliqué.
Ayant seulement un niveau de terminale S en physique, j’ai du mal à trouver des sites qui parlent « simplement » de la physique quantique, sujet qui me passionne énormément.
J’ai bien compris que l’impossibilité de déterminer simultanément avec précision la position et la vitesse d’une particule se traduit par le fait que les matrices correspondantes ne commutent pas. A*B est différent de B*A. Ok (un peu comme un Rubik’s Cube avec 2 rotations successives de 2 faces adjacentes si j’ai bien compris).
Mais je ne comprends pas pourquoi on effectue justement le produit d’une matrice A (correspondant aux vitesses) par une matrice B (correspondant aux positions)? Dans quelle formule on effectue cette multiplication? Que donne la matrice résultante de ce produit? Je ne comprends pas le raisonnement.
D’une façon générale, pourquoi multiplier ensemble les matrices de grandeurs complémentaires? Et à quoi correspondent les coefficients de ces matrices?
Un immense merci!
quentingarcon
28 août 2017 à 21 h 55 minHello Jerôme ! Je te renvoie au mail que je t’ai envoyé avec bien plus de détails que je ne saurai en donner par commentaire !