Vous voulez apprendre des trucs physiques pour vous faire de l’argent sur le dos des gens moins curieux que vous ? Alors c’est parti !
Attention, ça frotte !
Physiquement, les frottements (ou frictions) sont des forces qui s’opposent au mouvement de deux solides en contact l’un par rapport à l’autre (on parle de mouvement relatif) et la discipline qui les étudie est la tribologie.
Par exemple, prenez un objet plat et mettez le sur une surface inclinée (une boîte d’allumettes sur votre main). Vous remarquez que l’objet ne se met pas immédiatement à glisser à peine vous penchez votre main ? C’est grâce aux frottements que votre boîte ne vient pas se suicider au sol.
Sans entrer dans les détails, plus la surface penche, plus l’objet est susceptible de glisser. En effet, il existe un angle limite dépendant de la surface avant que ça ne tombe. Je renvoie les curieux vers les Lois de Coulomb.
Money timeeeee !
Voila la première expérience. Prenez une bouteille. Disposez sur l’ouverture un billet. Je suggère 10€ pour ne pas risquer de perdre beaucoup. Par dessus le billet, sur l’ouverture demandez à votre vict… compagnon de boisson de mettre une pièce. S’il réussit sans toucher les pièces, ni les faire tomber, à retirer le billet, alors il le gagne. Sinon vous gagnez toutes les pièces qui tombent.
Comment faire ? On se lèche l’index (le votre, pas celui de l’autre personne qui risquerait de trouver cela étrange) pour rendre votre doigt plus adhérent au billet. Puis, d’un coup sec vers le bas, on frappe le billet sur la partie qui dépasse (sinon avec la bouteille dessus, c’est vite douloureux). Et comme vous êtes gentils, je vais le faire pour vous :
Vous voulez gagner plus d’argent ? Voila l’expérience numéro 2. Toujours la bouteille, toujours le billet mais dans l’autre sens. La billet est sur la table, la bouteille est sur le billet ouverture vers le bas. Votre mission, si vous l’acceptez est de retirer le billet. Sans toucher ni faire tomber la bouteille.
Solution : faîtes rouler. C’est le meilleur moyen.

Explication simplifiée : Les pièces, le billet et la bouteille ont une position plutôt stable dans leur vie. Ils n’ont pas spécialement envie de suicider. Par conséquent, il y a des frottements qui les empêchent d’être séparés. Sauf si vous jouez sur une force tangentielle.
Vive l’équilibre !
C’est grave docteur ?
Savez-vous exactement ce qu’est le centre de gravité ? Ce point, souvent nommé G en physique (aucune blague malsaine ne sera acceptée) est bien utile. Globalement, en terme de poids et de gravité, vous êtes physiquement équivalent à un point. Sans offense.

Ici, en trouvant le centre de gravité de la barre, l’enfant peut le faire tenir en équilibre.
Cela veut dire que pour étudier votre corps en chute libre, un seul point suffit et c’est très souvent le cas en physique. Avec ces notions, on se rend compte qu’une force quelconque peut être appliquée directement à ce point.
Pour mieux comprendre, imaginez qu’une force telle que le poids est une flèche orientée vers le centre de la Terre (en gros c’est vers le sol). On appelle cela un vecteur. Cette force fait que vos objets aiment se suicider en se jetant contre le sol. Par exemple, si vous mettez votre téléphone portable sur le bord d’une table et que moins de la moitié dépasse de cette table, alors il ne tombera pas.
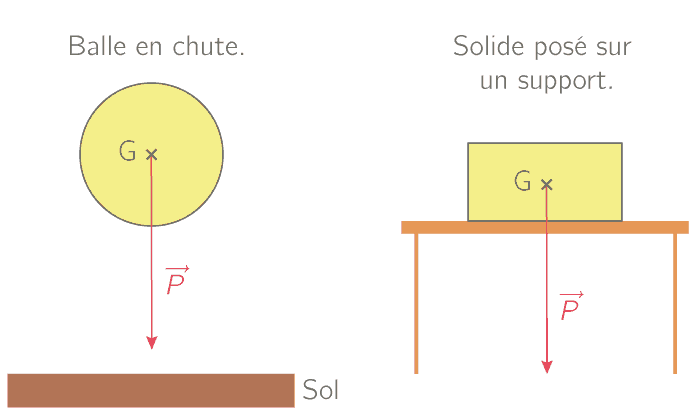
2 exemples de vecteur poids (source)
Maintenant, si vous faites en sorte que plus de la moitié de votre téléphone dépasse (ne le faîtes pas…), alors il tombe (vous étiez prévenus). Visualisez alors une flèche partant du portable visant le sol. Quand cette flèche est bloquée par la table alors l’objet est retenu. Si cette force est au-dessus du vide alors elle l’entraîne.
La grande question est alors : « Mais cette flèche, elle démarre d’où ? »
S’il y a plusieurs objets et que vous cherchez le centre d’inertie global en connaissant le centre d’inertie de chacun nommé ![]() :
: ![]()
Cependant, pour notre cas si vous n’en cherchez qu’un seul dans votre solide S alors il va falloir sortir l’artillerie lourde si l’objet est complexe : ![]() .
.
Et cette mignonne formule va vous donner un point. En réalité, c’est plutôt simple quand la forme du truc à observer est très géométrique et homogène en masse (que la masse est répartie de façon équitable).
Le résultat est même très intuitif. Par exemple le centre d’inertie d’un cercle est son centre. Celui d’un carré ou d’un rectangle est le point d’intersection de ses deux diagonales. Pour une sphère, c’est son centre. Pour un parallélépipède (une boîte), c’est pareil que le carré puis vous montez de la moitié de la hauteur.
Bon pour votre corps, à moins que vous ne soyez un cylindre ou une boule, c’est de suite plus complexe aux premiers abords. Mais pourtant, de façon assez intuitive, votre centre d’inertie va se trouver vers la moitié de votre corps en hauteur (il est plus bas chez les femmes que chez les hommes de quelques centimètres). Et environ à la moitié de votre épaisseur aussi. Considérez que tant que votre centre d’inertie possède quelque chose en dessous pour le soutenir (vos jambes par exemple) alors vous ne tomberez pas. Sinon il vous faudra soit compenser avec vos muscles (principe du gainage), soit tomber.
2 autres expériences d’équilibre

Cette fois-ci, pas de solution, c’est juste impossible. Vous accuserez donc vos victimes de ne pas avoir assez d’équilibre !
Expérience 1 : Debout face à un mur avec les doigts de pieds qui touchent le mur, la victime doit se mettre sur la pointe des pieds sans décoller les doigts de pieds du mur. Personne ne tient plus de 3 secondes.
Explication 1 : Vos pieds vous offrent une surface de contact assez grande pour tenir droit sans tomber en avant. Mais en soulevant les talons, votre centre d’inertie, normalement au-dessus de vos jambes dans la continuité des talons, se retrouve au-dessus du vide. C’est la chute des corps !
Expérience 2 : Debout à côté du mur. Collez la joue de la victime contre le mur ainsi que le pied (du même côté que la joue) contre ce même mur. Elle doit désormais lever la jambe opposée.
Explication 2 : C’est encore plus vicieux vu le poids d’une jambe mais c’est le même principe. Votre centre d’inertie va cette fois-ci être déplacé. En effet, en levant la jambe, vous emmenez de la masse vers celle-ci. Votre centre d’inertie la suit donc. Et dès qu’il est au-dessus du vide ? Vous connaissez la suite.
Mais pourquoi le mur ? Sans le mur, plus rien ne fonctionne. Il vous empêche de naturellement mettre du poids de l’autre côté pour maintenir votre équilibre (tendre ses bras dans la direction opposée de la chute par exemple).
Conclusion
A part pour arnaquer, ce genre de petits jeux passent très bien dans de nombreuses occasions et amuseront vos connaissances.

5 Commentaires
Chaprouge
17 juillet 2017 à 21 h 35 minVicieux mais très rigolo et très bien expliqué . Félicitations c’est très intéressant
quentingarcon
28 août 2017 à 21 h 58 minMerci !
tingascio
28 septembre 2017 à 11 h 53 minTrès bon article ! Très bien expliqué !
Merci pour les idées. Ça me permettra de faire la maligne à l’occasion en société ^^
quentingarcon
30 septembre 2017 à 11 h 06 minEt d’arnaquer des gens. C’est toujours bien vu en société !
Éventuellement de gagner un petit pari ou deux, c’est encore mieux.
Patrick Jane Fullbuster
29 janvier 2018 à 1 h 08 minOMG j’ai 17 ans ma mère est plus tôt spécialisé dans l apprentissage mais paradoxalement, elle ne supporte pas que je lui apprennent des choses avec ce magnifique tour je vais l’épater 🙂 *.* encore Mercis. ?❤